2021-05-17
选择题
第1题
知识点1
设A为任一命题公式
重言式(永真式):A在它的各种赋值下取值均为真
矛盾式(永假式):A在它的各种赋值下取值均为假
可满足式:非矛盾式则为可满足式
重言式一定是可满足式
知识点2
- 蕴含式:p->q
- 只有p为真且q为假时p->q为假
- 合取式:p∧q
- 只有p和q都为真的时候p∧q才为真
- 析取式:pVq
- 只有p和q都为假的时候pVq才为假
- 否定式:非p
- p为真,非p为假的
- 蕴含式:p->q
解题 B
找出一种赋值下结果为假即可排除
A. P=1,Q=0;P->Q为假,P->(P->Q)为假
B. 要想整体为假,则Q必须为0,前部分整体为真,即P必须为1;
将P=1,Q=0带入发现整体为真,因此为永真式
c. P=1,Q=0
D. P=1,Q=0
第2题
判断各非负整数列是否可简单图化
- 非负整数列之和为偶数才可图化
- 最大度<=顶点数-1
- 根据度数画出图观察是否为简单图
简单图:不含平行边和顶点自身的环
解题 D
- 根据1排除B,根据步骤2排除A,根据步骤3排除C
第3题
知识点(P125)
自反: 如果a是A的元素,那么<a,a>是R的元素
每个顶点都有环
反自反:如果a是A的元素,那么<a,a>不是R的元素
每个顶点都没有换
对称: 如果<a,b>是R的元素,那么<b,a>是R的元素
反对称:如果<a,b>,<b,a>是R的元素,那么a,b相等
只有单向边
传递: 如果<a,b>,<b,c>是R的元素,那么<a,c>是R的元素
解题 D
A:反自反
B:反自反
C:传递性
第4题
解题 D
集合中可定义多少个不同的等价关系
- 集合划分,举例说明
- A={1,2} (总计2个等价关系) {[1],[2]} | {[1,2]}
- A={1,2,3} (总计5个等价关系) {[1],[2],[3]} | {[1,2],[3]} | {[1,3],[2]} | {[2,3],[1]} | {[1,2,3]}
为方便辨认,将集合内部集合的{}用[]进行替换
第5题
知识点
- 和第一题一样
- 可将00,01,10,11分别代入看有几个真
解题 C
第6题
知识点(P8)
- 命题必须是陈述句 排除A
- 命题必须能确定真假 排除B(B无法确定真假)
- 当且仅当:<->(等价联结词)
- p<->q只有当p和q都为真或都为假的时候才为真
- 只有…才….:–>(蕴含联结词)
- 只有p为真,q为假是p–>q才为假
解题 此题感觉都不符合
- C选项p为真,q为假,整体为假
- D选项p为真,q为假,整体为假
第7题
知识点(P301)
点割集:删除某几个点能够使得图的连通分支增加的点集合
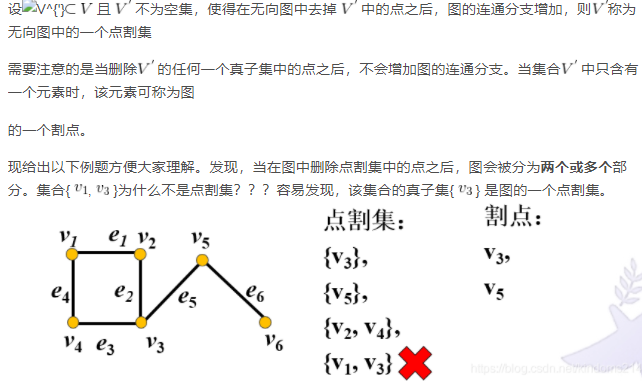
点连通图:使连通图G成为一个不连通图需要删除的点的最小数目,记为K,则图也可称作K-连通图
边连通图:使连通图G成为一个不连通图需要删去的边的最少数目,记为R,则图也可称作R边-连通图
彼得森图:
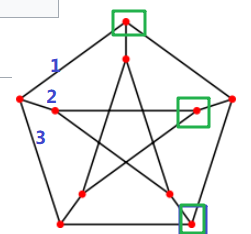
解题 A
- 删除上图中紫色的3条边可以使得此图不再连通
- 删除绿色框框标记的3个点可以使得此图不再连通
第8题
知识点(P113)
- 恒等关系l(A)={<x,x>|x属于A}
- 全域关系E(A)={<x,y> | x属于A并且y属于A}=*AA**
- (集合之间相乘)
- A={a,b},B={c,d}
- A*B={<a,c>,<a,d>,<c,a>,<c,d>}
解题 D
求出全域关系后和第一题知识点一样
第9题
- 知识点
- 欧拉公式:边划分的区域数+顶点数=边数+2
- 解题 D
第10题
知识点
- 集合和集合之间是包含关系,注意{a,b}属于{a,b,{a,b}}也是正确的
解题 C
填空题
第1题
- 知识点(P50) 推理公式
- 解题: A->C
第2题
- 知识点:直接除以7模是3组成的集合
- 解题: {3,7}
第3题
知识点
以图G为例子
- 连通图:图G是平凡图或者任何两个顶点都是连通的
- 平凡图:只有一个结点的图
- 强连通图:有向图中任意两个顶点中存在互相连通的路径
- 哈密顿图:拥有哈密顿回路的图
- 哈密顿回路:经过图中所有顶点一次且仅一次的回路
- 连通图:图G是平凡图或者任何两个顶点都是连通的
答案:假,0–>不一定存在回路
第4题
知识点:P64,P75
解题:∃x(F(x)–>G(x))
第5题
知识点:P95
- A⊕B=(A-B)U(B-A)
- A⊕A=(A-A)U(A-A)=Ø
解题:Ø
第6题
知识点:P92
- 看答案有四个,一般会认为只有三个
解题:{Ø,{Ø},,{Ø,{Ø}} }
第7题
知识点:P74
- 直接根据书上的公式进行变化
- 前束范式:Q1X1Q2x2…Q(k)x(k)
- 注意前束范式的形式即可
解题:∀x∃y(¬F(x,y))
第8题
- 知识点:P307
- 二部图:将图的节点V分为两个节点集V1和V2,图中每条边的两个端点都是一个属于V1,另一个属于V2
- 完全二部图:V1中每个顶点均与V2中的每个顶点相邻,即V1中每个顶点和V2中的所有顶点之间都存在边
- 欧拉回路(P316):通过图中所有边一次且仅一次行遍所有顶点的通路
- 因此这个题就是求图总共有多少条边
- 解题:r*s
- 完全二部图,所以将图中顶点分为V1和V2,然后V1中所有顶点和V2中的所有顶点之间都存在边
- 因此总共含有的边数就是:V1*V2
第9题
知识点:P74
- 做题时候直接翻书带公式
解题:∀xA(x)∧B
第10题
知识点:P297
- 任何无向图中所有顶点的度数之和是边数的两倍
- 任何有向图中所有顶点的度数之和是边数的两倍,所有入度之和等于出度之和等于边数
解题: 7
10条边:因此所有顶点度数之和为20,减去已知度数(3 * 2+4 * 2=14),剩余6
已知其余顶点的度数都小于3,求至少的顶点数,因此假设其余顶点度数为最大,小于3因此取2,
6/2=3,其余顶点数为3,因此所有顶点数之和为7
解答题
第一题
P28-P29
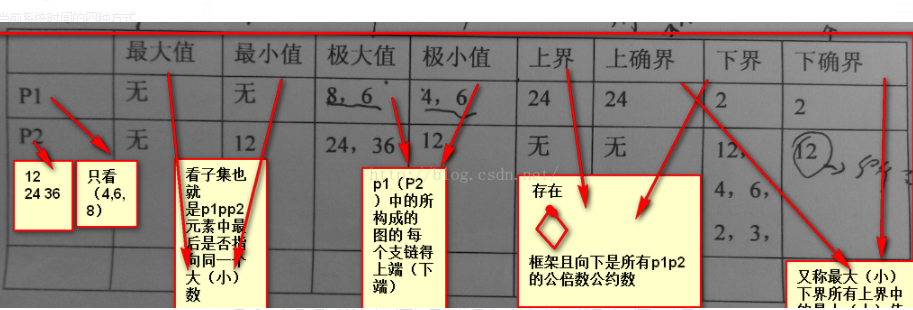
第二题
- 哈斯图相关知识点介绍
第三题
根据哈斯图进行求解
第四题
P22等推理公式进行求解